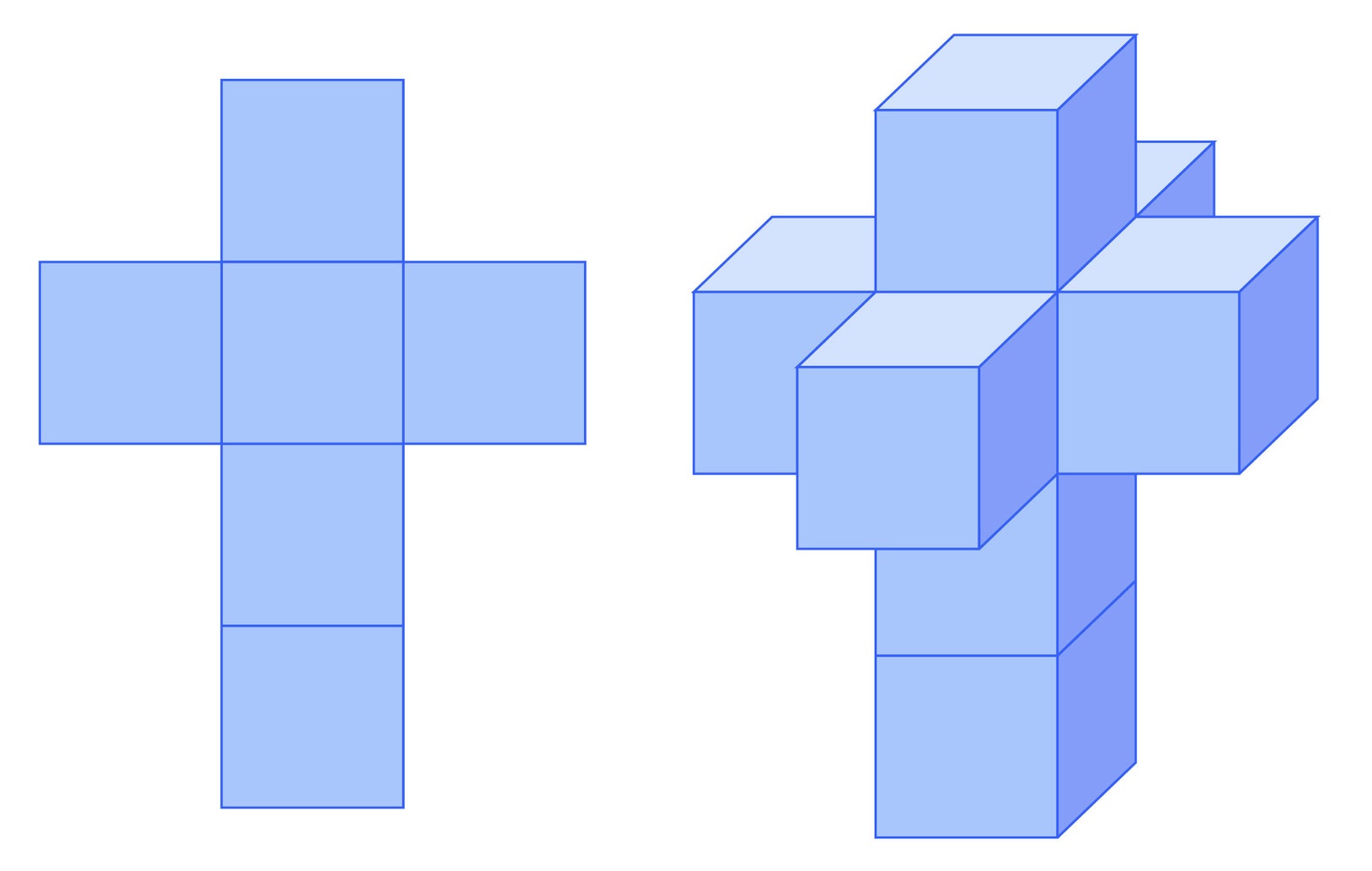
Alternatively, just as we can unfold the faces of a cube into six squares, we can unfold the three-dimensional boundary of a tesseract to obtain eight cubes, as Salvador Dalí showcased in his 1954 painting Crucifixion (Corpus Hypercubus).
We can envision a cube by unfolding its faces. Likewise, we can start to envision a tesseract by unfolding its boundary cubes.
This all adds up to an intuitive understanding that an abstract space is n-dimensional if there are n degrees of freedom within it (as those birds had), or if it requires n coordinates to describe the location of a point. Yet, as we shall see, mathematicians discovered that dimension is more complex than these simplistic descriptions imply.
The formal study of higher dimensions emerged in the 19th century and became quite sophisticated within decades: A 1911 bibliography contained 1,832 references to the geometry of n dimensions. Perhaps as a consequence, in the late 19th and early 20th centuries, the public became infatuated with the fourth dimension. In 1884, Edwin Abbott wrote the popular satirical novel Flatland, which used two-dimensional beings encountering a character from the third dimension as an analogy to help readers comprehend the fourth dimension. A 1909 Scientific American essay contest entitled “What Is the Fourth Dimension?” received 245 submissions vying for a $500 prize. And many artists, like Pablo Picasso and Marcel Duchamp, incorporated ideas of the fourth dimension into their work.
But during this time, mathematicians realized that the lack of a formal definition for dimension was actually a problem.
Georg Cantor is best known for his discovery that infinity comes in different sizes, or cardinalities. At first Cantor believed that the set of dots in a line segment, a square and a cube must have different cardinalities, just as a line of 10 dots, a 10 × 10 grid of dots and a 10 × 10 × 10 cube of dots have different numbers of dots. However, in 1877 he discovered a one-to-one correspondence between points in a line segment and points in a square (and likewise cubes of all dimensions), showing that they have the same cardinality. Intuitively, he proved that lines, squares and cubes all have the same number of infinitesimally small points, despite their different dimensions. Cantor wrote to Richard Dedekind, “I see it, but I do not believe it.”
Cantor realized this discovery threatened the intuitive idea that n-dimensional space requires n coordinates, because each point in an n-dimensional cube can be uniquely identified by one number from an interval, so that, in a sense, these high-dimensional cubes are equivalent to a one-dimensional line segment. However, as Dedekind pointed out, Cantor’s function was highly discontinuous—it essentially broke apart a line segment into infinitely many parts and reassembled them to form a cube. This is not the behavior we would want for a coordinate system; it would be too disordered to be helpful, like giving buildings in Manhattan unique addresses but assigning them at random.