I’m not sure if you understand how many physicists watch baseball, but it’s a lot. I think it’s so popular with us because there are some very basic principles at work. You can model the motion of a simple fly ball in your introductory-level class, but you can also make it much more complicated (and fun). So with that in mind, let’s consider the following question: Just how in the heck does a baseball player even catch a fly ball?
When a batter hits a ball, it can hurtle through the air for three to six seconds before falling into the outfield. That gives an outfielder only moments to calculate its landing location. Do you think they crack out a textbook and look up the equations for projectile motion? No way. But the player is using physics. Here’s what’s going on.
Catching a Ball the Physics Textbook Way
First, let me just find the landing location of a ball using physics. After that, I will solve this problem the way a player might do it in an actual game.
But let’s make two assumptions about this ball. First, there will be no air resistance on it. (It will just be easier to calculate without air resistance. Also, in many cases with low ball speeds, this approximation is fairly legit.) Second, I’m going to make this two-dimensional (instead of 3D). The ball is going to be launched in a line straight towards the player in the outfield. That way, I don’t have to worry about the player moving side to side in order to catch the ball, just back and forth.
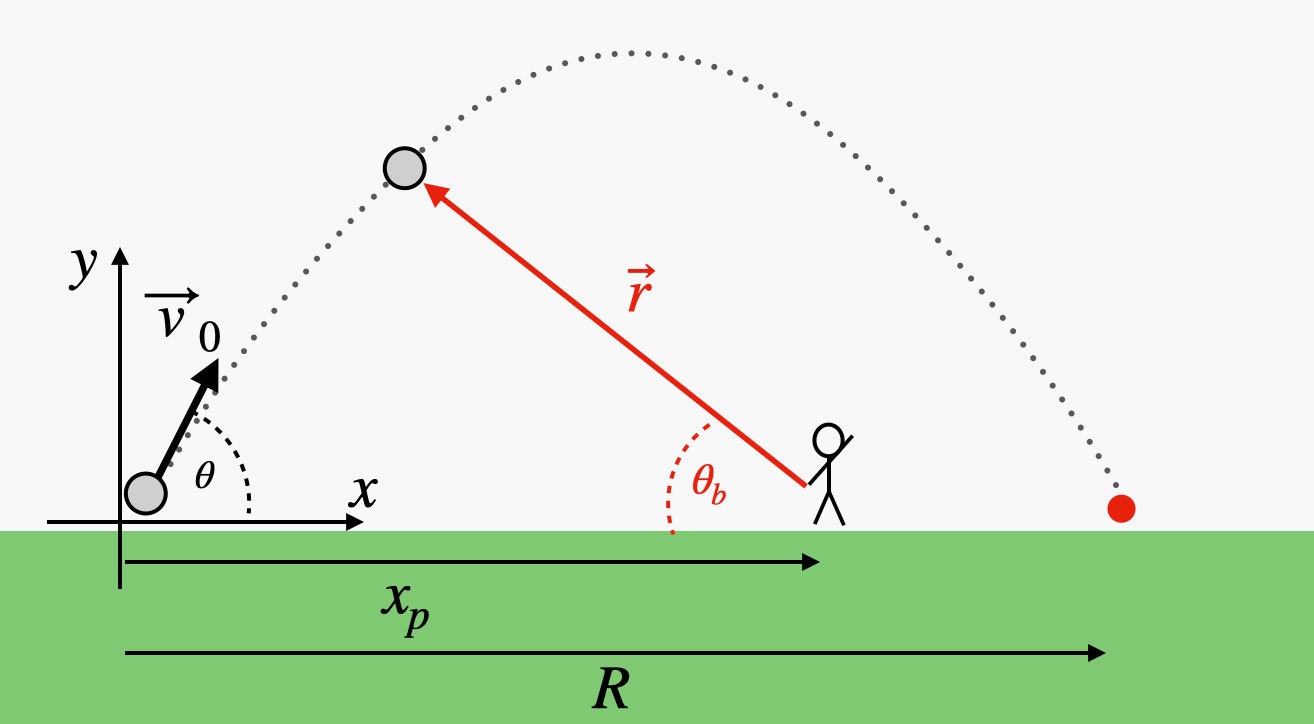
This problem has a bunch of variables, so let me start off with a diagram showing all these quantities. I’m going to assume the ball is launched from the origin such that it travels along the x-axis.
Illustration: Rhett Allain
There’s a lot of stuff here, so let’s describe each variable.
- v0 is the starting velocity of the hit baseball.
- θ is the launch angle of the ball.
- xp is the starting position of the player (along the x-axis).
- R is the final x-position of the baseball when it returns back to ground level.
- Finally, there is the vector r. This is a vector from the location of the player to the location of the ball (in the air). The angle θb is the angle of this vector with respect to the ground.