A New Proof Moves the Needle on a Sticky Geometry Problem
A deceptively simple math proposition known as the Kakeya conjecture underpins a tower of other questions in physics, number theory, and harmonic analysis. ..
A deceptively simple math proposition known as the Kakeya conjecture underpins a tower of other questions in physics, number theory, and harmonic analysis. ..

A decades-old conjecture about the best way to minimize the surface area of a three-bubble cluster seemed unprovable—until a breakthrough result. ..

Mathematicians predicted that if they imposed enough restrictions on how a shape might tile space, they could force a periodic pattern to emerge. They ..

Recent explorations of unique geometric worlds reveal perplexing patterns, including the Fibonacci sequence and the golden ratio. ..

In 1973, Paul Erdős asked if it was possible to assemble sets of “triples”—three points on a graph—so that they abide by two seemingly incompatible ..
More than 30 years ago, Andreas Floer changed geometry. Now, two mathematicians have finally figured out how to extend his revolutionary perspective. ..

The result could help researchers answer a larger question about flattening objects from the fourth dimension to the third dimension. ..

The n-queens problem is about finding how many different ways queens can be placed on a chessboard so that none attack each other. ..
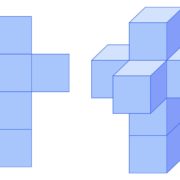
The concept of a dimension seems simple enough, but mathematicians struggled for centuries to precisely define and understand it. ..

Researchers are turning to the mathematics of higher-order interactions to better model the complex connections within their data. ..