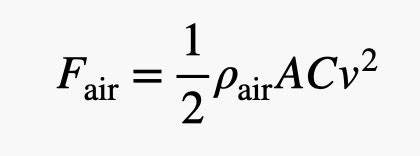Using known values for volume, density of air, and the gravitational field, this gives a buoyancy force of 11.8 newtons, or 2.7 pounds.
Now, let’s replace that block of air with another block that’s identical in shape and size. But this time, suppose it’s 1 cubic meter of water with a density of ρwater = 1,000 kg/m3.
Since it has the same volume as the floating air, this block will have the exact same buoyancy force. It doesn’t matter what you put in that space, if it has a volume of 1 m3, it’s going to have a buoyancy force of 11.8 newtons. But for this cube of water, that’s not enough to let it float. The gravitational force pulling it down will be much larger—it’s 9,800 newtons. The water cube is just going to fall.
In order for buoyancy to be greater than the gravitational force, you need to fill that space with a substance with a density that’s lower than air’s. There are two common methods to get this to work in real life. One is to use a thin rubber container filled with a low-density gas. (Think of a helium balloon.) The other is to use a low-mass container to hold hot air, which is less dense than cold air and will rise above it. (Think of a hot-air balloon.)
So if you want a cloud to float, it has to have a density lower than that of air. But how can that density be lower if the cloud contains both air and water?
It’s because clouds don’t really float.
Why Does the Size of Water Matter?
Let’s say that a cloud consists of air plus a bunch of very tiny water drops. The size of the drops is important. You might be surprised to learn that even if they are both made of water and have the same shape, small drops don’t behave like large drops. In order to understand the difference between them, we need to look at air resistance.
Let’s start with a quick demonstration. Stretch out your arm in front of you with your hand open. Now swing your arm back and forth so that your hand moves quickly through the air. Do you feel anything? It might be slight, but there should be an interaction between your hand and the air, a backwards-pushing force that we call air resistance or air drag. (You will definitely notice it if you stick your hand out the window of a moving car.)
We can model the air resistance on a moving object with the following equation:
Illustration: Rhett Allain