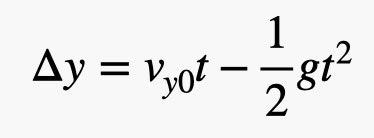Sometimes crazy things happen—so crazy they don’t even seem real. Last week, Phillies right fielder Bryce Harper was warming up before a game with some practice bats. He hit a nice line drive, and then it collided with another ball in midair. That gives us some fun physics to unpack. Let’s see how unlikely this event is.
What Data Can We Get From the Video?
There are two balls involved in this crash. Harper’s probably started its flight at home plate. I’m going to call this ball A. The second one was thrown toward home plate by a player somewhere in the outfield. Let’s call this ball B. I need to get a value for where the balls start, what their velocities are, and where they collide. The Major League Baseball clip that I linked to before is not the best video, in that it doesn’t show the complete trajectories of either ball, so we may just have to approximate some stuff.
One thing that we can see is the impact between the two balls, which happens above second base. Afterwards, it appears that ball B falls straight down and lands near the base. But how high above it is the point of impact? By watching the video, it’s possible to get an approximate free fall time for ball B. (I’m going with 1.3 seconds, based on my measurements.) If I know the time it takes to fall, and that the vertical acceleration is -9.8 meters per second squared (because this is happening on Earth), then I can find the falling distance using the following kinematic equation:
Illustration: Rhett Allain
With my estimate for the falling time, I get a collision height of 8.3 meters. If the baseball field is in the x-z plane and the position above the ground is the y direction, that means I now have all three coordinates for the collision point: x, y, and z. I can use this point to find the launch velocity of ball A. I know that it starts moving at home plate, which is 127 feet from second base. So I’ll put my origin at home and then let the x axis be along a line between home and second.
Now I just need the initial velocity vector for ball A such that it passes through the collision point. There are several ways to find this, but the simplest is to just use Python to plot the trajectory of the ball and adjust the launch angle until it “hits” the collision. I’m going to use a starting ball velocity (the exit speed) of 100 miles per hour. (That’s 44.7 meters per second.)